撰文:CertiK

ZK 的崛起与演变
曾几何时,零知识证明(以下简称 ZK)仍然被认为是密码学教科书中的理论概念,至少在传统安全研究中很少被主流社群深入探索。然而在 Web3.0 领域,区块链技术的迅速发展,用短短几年时间实现了 ZK 从理论到实践的跨越式进展,一路蓬勃,高歌猛进。
1985 年诞生,2014 年 ZCash 才用 SNARKs 证明了 ZK 不仅是书本上的传说,也是实打实的「江湖绝学」,2019 年开始,随着 zkSync 和 Polygon 的崛起,ZK 从隐私保护的小众技术,摇身一变成了区块链扩展性问题的关键。到了 2022 年,Tornado Cash 轰然倒下,美国财政部的制裁引发了一场关于隐私与自由的广泛讨论,也让 ZK 成为了茶余饭后的热门话题。2023 年起,随着 PLONK、Halo2 等新型 ZK 协议的成熟,ZK 技术在区块链领域高速发展,成为 Web3.0 的新宠。
ZK 的崛起不仅仅是因为它在区块链世界中的广泛应用,也与这些年来不断创新的开发工具密不可分。尽管这些工具的核心目标都是将代码逻辑电路化,但几年间,从最初合约级应用的 Circom,到链上层为性能优化推出的 EVM 兼容或等价的 zkVM,更新速度之快令人目不暇接,甚至连应用生态脚步都还没稳住,下一次升级迭代已呼啸而至。
ZK 原理概述
想理解 ZK,可以从其共性的漏洞入手。在传统安全里有个经验:直接分析代码逻辑来理清全局往往难度极大,有时不如跑个 crash 看 dump 来得直观,也就是通过漏洞回溯代码的方式去理解内在逻辑。
初识 ZK,可能会被各种专有名词包围 — SNARK、STARK、PLONK、QAP、R1CS、Groth16。这些名词乍听还可理解,一旦深入探究,就会发现背后需要扎实的数学功底。所以,很多介绍 ZK 的内容,要么是光彩夺目的概念科普,要么是晦涩难懂的协议分析,仿佛置身于一片高深莫测的领域。今天这篇文章,希望能带给你一种不同的体验。我们将从一个简单的除法证明问题出发,从工程实践的角度带你走近 ZK 的世界线。
在我们讨论后续问题之前,我们先用一个实践向的直观视角来解释一下 ZK,以便后续讨论时有一个共同的基础。在智能合约和区块链中应用 ZK 技术解决的核心问题是如何在不暴露答案本身的情况下,证明自己知道这个正确的答案,例如一个多项式方程的解。越过原理,只想说目前有成熟方法能够实现这个目标:首先,将一个复杂的问题通过多个仅涉及乘法和加法的简单问题加以描述;然后,将这些简单问题转换为矩阵和代表正解的 witness 相乘的形式;接下来,将矩阵转化为 verification-key;同时,witness 则进一步转换为 proof。
简而言之:一个复杂问题被转化为一组特定的 key,而答案被分解为多个 witness,最终演变为 proof;proof 能够用 verification-key 以固定的算法验证。一方面验证成功说明生成 proof 的人确实知道问题的正确答案,另一方面通过 proof 却无法反推出原解,保护了隐私。这一验证过程可以用于提款的同时不暴露存款凭证;也可以用于证明一个 transaction 引发的合约代码执行结果的真实性,进而用短 proof 代替多人执行 transaction 造成的资源消耗。
约束挑战
由于 ZK 所有相关计算都在椭圆曲线上进行,只有加法和乘法是直接定义的。要证明一个复杂问题,必须将其拆解成包含这些基本运算的简单子问题,即电路化。电路化的过程也是目前出问题最多的地方。
拆分出来的简单的子问题被称为「约束」,它们联立后必须与原始复杂问题等效。如果某个约束缺失,可能导致构造出符合所有约束但不是正确答案的 witness,从而伪造证明。这些伪造的证明仍然能够通过 verification-key 的检查,带来一系列严重后果:如合约级别的双重支付、或者 zkVM 级别的修改计算中间结果等。另一方面,若约束过于严格,超出了原问题的需求,则可能导致无法找到合适的 witness,进而导致交易无法被证明,造成链级别的拒绝服务攻击或合约应用的功能失效。第一种利用欠约束伪造证明看起来更有趣,它相当于直接控制了执行过程,类比于传统安全漏洞利用时的控 PC 指针。
除法的案例分析
下面就来看一个简单的除法问题在 ZK 的语境下该怎么约束,又能惹出多少乱子。
设想如下场景,zkVM 在运行时,执行了一个 a 除以 b 的运算,且我们要证明商是 q,余数是 r。在这里,a、b、q、r 都是 witness,我们需要确保它们满足除法的约束。假设 a 和 b 已经由前序执行过程约束确定,我们仅关注 q 和 r 的约束。直觉上,既然 a=b*q+r 是除法的乘法表达形式,是不是一个约束多项式就够用了呢?绝对不是!在实际的工程实现中,情况要复杂得多。例如,zkSync 曾经的除法验证过程涉及的代码如下:
首先,a(src0_view)和 b(src1_view)通过 allocate_div_result_unchecked 计算出 q 和 r,这部分仅仅是算数运算,先验地根据 a 和 b 求出作为 witness 的 q 和 r,不涉及约束。

出于优化考虑,zkSync 将乘法和除法放在同一个函数里进行约束,所以接下来是根据乘或除,通过带有约束的选择器取出要约束的变量,即 r、q、b、a,并增加乘法约束 MulDivRelation,也就是要求 a=b*q+r。

MulDivRelation 的乘法约束在指令循环即将结束前才由 enforce_mul_relation 函数施加。然而,由于 zkSync 选择了 Goldilock 域(域阶为 0xffffffff00000001),这个域空间并不足以表示所有的 uint64 类型数据。因此,uint256 需要分解成八个 uint32 来记录。为了处理这部分的乘法,系统采用了逐轮计算的方式,每一轮通过 fma_with_carry 门对两个 uint32 执行乘法约束。

乘法结束时,先用一次 enforce_equal 门约束计算结果没有进位,再用一次保证乘加的累积结果和 a 相等。第二个 enforce_equal 的目的容易理解,也就是用于满足我们之前反复提及的 a=b*q+r。

第一个没有进位的约束确保了商 q 和余数 r 的值不会超出预期的范围,避免了计算结果出现溢出。除了进位检查,另一个常用方法是约束比特长度(通过限制商和余数比特数,确保计算的结果符合预期的范围)。zkSync 记得带上了这个约束,但其实这是个很容易被忽略的细节,比如 renegade 项目计算 fee 相关用到的除法就漏掉过这个约束:
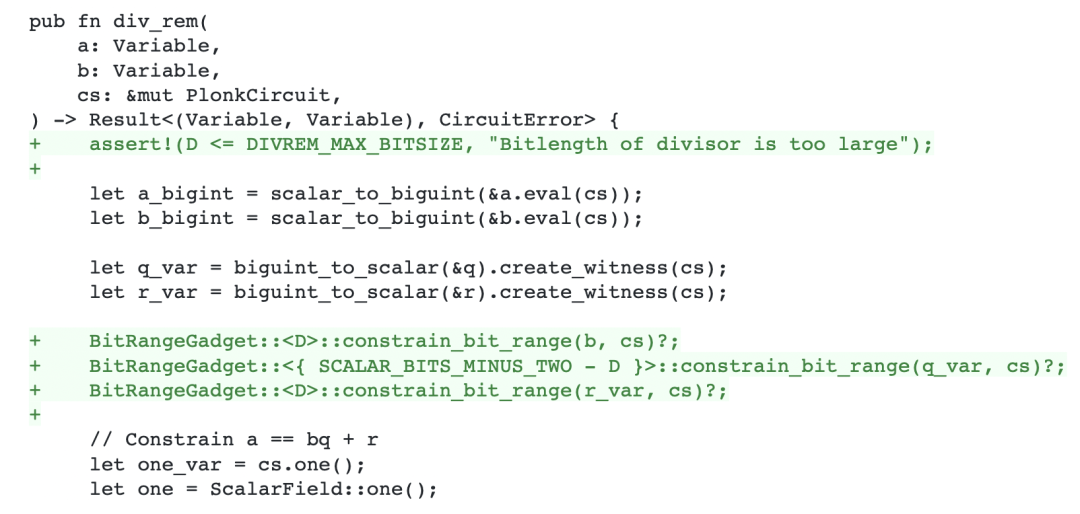
再比如 Circom 中的大整数求模库函数 Bigmod 也曾出现过类似的漏洞。具体来说,Bigmod 函数在实现过程中,只检查了商 q 的比特长度,而忽略了对余数 r 的长度检测:

之所以要有这个约束,是因为有限域内的溢出会让结果回滚仍落入域内,使得 q 和 r 不唯一。比如给定一个新的 r'=r-k,总能通过 q'=(a-r')*b^(-1) 计算得到一个满足条件的 q'使攻击者修改除法计算结果。对于日常使用的 a 和 b,这样修改 r 通常会导致一个非常大的 q。
在 zkSync 的代码中,乘法约束的设置只是第一步。接下来,它要比较 r 和 b(除数),确保 r<b。具体来说,allocate_subtraction_result_unchecked 执行了这一比较操作,它做的只是计算出 r-b,并将结果存入变量 subtraction_result_unchecked 和 remainder_is_less_than_divisor。其中 remainder_is_less_than_divisor 记录了长减法是否发生了借位。借位了则意味着 r<b,这是我们期望看到的情况(由 conditionally_enforce_true 约束保证正确性)。之后 b、r-b (subtraction_result_unchecked)、r、of (remainder_is_less_than_divisor) 会被放入 AddSubRelation。

在指令循环结束前,通过 enforce_addition_relation 函数施加 UIntXAddGate 加法门约束。确保 (r-b)+b=r+of*2^256,其中 of 代表的是加法过程中产生的进位。这个约束的逻辑在于,r-b 的结果应该为负数,域内表现为一个非常大的正数。为了让这个结果能够被正确表示,r-b 与 b 相加时,必然会超过 2^256 导致进位,使得 remainder_is_less_than_divisor 的约束得以满足:

这么一套约束的目的是避免攻击者通过构造另一组商 q'和余数 r'来绕过除法约束,进而伪造计算结果。比如我们设定新的 q'=q-k 和 r'=r+b*k,很容易就找到了一组也符合乘法关系的 witness 篡改计算结果。这个约束在实际代码中也很容易被忽略。例如,Polygon 项目就曾经在代码中误加了过于宽松的 r<a 约束:

在 zkSync 的除法计算过程中,表面上看似乎所有必要的约束都已经施加,但代码实现上仍然存在漏洞。这个漏洞和 zkSync 的代码设计相关,之前提到,uint256 类型的数据是通过八个 uint32 表示的,而每个 uint32 背后实际上是 variable 类型,它代表的是 Goldilock 域中的元素。因此,每个 variable 实际上最大可以表示 0xffffffff00000000。
如果希望 uint32 中的 variable 仅表示 32 位整数,则必须为每个 uint32 额外施加比特长度约束,以确保其数值范围受限。但在 allocate_subtraction_result_unchecked 函数中,并没有对计算结果 subtraction_result_unchecked 中的每个 uint32 施加这种比特长度约束。这意味着,虽然 subtraction_result_unchecked 被定义为[uint32; 8],但其中每个 uint32 实际上表示的最大值是 0xffffffff00000000,而不是期望的 32 位限制。
因此,如果把 subtraction_result_unchecked 中最后一个 uint32 的第 32 比特篡改为 1,则后面加法门的计算过程中必然会有进位,使得 remainder_is_less_than_divisor 约束天然满足。之后令 r'=r+b*k 和 q'=q-k 就可以产生同样合法的 q 和 r 的组合了。
总结
通过探讨除法约束在工程实现中一些 tricky 的细节,我们初步感受了一下 ZK 世界的复杂与精妙。每个细节都可能隐藏着影响整个系统安全性的潜在风险,也正是这些细微之处构成了 ZK 证明技术的核心,推动了其在区块链领域的广泛应用。未来的篇章里,CertiK 会继续深入 ZK 的技术细节,敬请期待。















